Choque entre dos Coches
Comúnmente solemos ver cómo se da el accidente del Choque entre dos Coches en el tráfico y sobre todo cuando vemos que uno de los conductores se distrae por ir revisando su SmartPhone lo cual resulta en un choque.
La siguiente situación es la típica, un coche choca a otro por alcance en un alto. El conductor empieza a frenar cuando ya se da cuenta que es demasiado tarde y logra impactar al coche que está esperando la luz verde en un alto de cierta esquina de la ciudad.

Como lo muestra la figura anterior, el conductor del primer coche va a una velocidad de 100 km/h cuando se percata de que una camioneta está detenida en un alto a 20 m de distancia. El conductor del Wolkswage presiona a fondo los frenos y el coche derrapa durante esos 20 metros. Supongamos que el pavimento es asfalto o alquitrán nuevo y seco entonces nos podemos referir a los coeficientes de fricción cinética dados en la tabla de mostrada aquí y elegimos nuestro caso.
Solución
Debido a que el primer coche va a 100 km/h seleccionamos un valor para el caso superior a los 50 km/h de la tabla. De esta forma para las condiciones vemos que el coeficiente de fricción cinética de este caso puede ser,
![]()
Además otro dato es que el primer coche tiene una masa de 700 kg en total. Así que con estos datos podemos calcular la fuerza de fricción cinética que surge cuando el coche empieza a derrapar en el pavimento.
![]()
Considerando que la calle por donde circulan tales coches se encuentra horizontal podemos calcular que la fuerza normal es igual a la fuerza de gravedad sobre el primer coche y está dada por,
![]()
Recordando que la g representa el valor de la aceleración de la gravedad en la Tierra cuyo valor es,
![]()
Sustituyendo los datos obtenemos que la fuerza normal es,
![]()
![]()
Ahora, como ya conocemos la Fuerza Normal podemos calcular la fuerza de fricción cinética con la siguiente fórmula,
![]()
Sustituyendo los valores del coeficiente de fricción cinética y de la fuerza normal tenemos que,
![]()
![]()
Cálculo de la Aceleración de Frenado
Entonces conocida la fuerza de fricción cinética podemos ahora conocer la aceleración negativa que le causa el frenado al coche. Usamos la Segunda Ley de Newton como lo dice la siguiente fórmula,
![]()
y de aquí al despejar la aceleración nos queda,
![]()
Sustituyendo en la fórmula anterior el valor de la fuerza de fricción cinética y el valor de la masa del primer coche tenemos que,
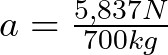
![]()
Cálculo de la Distancia de Frenado
Podemos calcular la distancia que requería en teoría el primer coche para recorrer hasta detenerse totalmente. La fórmula siguiente nos ayuda a calcular tal distancia que le toma al coche detenerse,
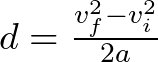
Pero antes se debe convertir la velocidad de km/h a m/s,
![]()
![]()
Ahora si, podemos sustituir en la fórmula de la distancia los datos de velocidad inicial, velocidad final y aceleración. Debes saber que la velocidad final es cero ya que se considera que se detuvo totalmente al recorrer la distancia que se va a calcular,
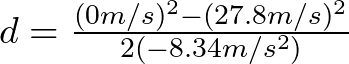
Puesto que la aceleración es un frenado, es decir, reduce la velocidad por cada segundo que pasa entonces se toma con valor negativo por esta razón. Si la aceleración aumentara la velocidad cada segundo entonces se tomaría como positiva. Así al hacer los cálculos tenemos que,
![]()
Como puedes ver, solo tenía 20 metros para frenar pero dada la velocidad con la que viajaba requería 46.33 metros y por ende se da el choque por alcance contra el segundo coche que estaba esperando la luz verde en el alto del crucero.

